Introduction
A vector is a quantity that has both a magnitude and a direction. Many of you will
have seen vector quantities before in high school math and physics. In linear algebra, vectors
can be interpreted both analytically (by numbers and variables) and geometrically (in a picture or graph).
A quantity with a magnitude but no direction is referred to as a scalar.
Scalars are denoted by lowercase letters, such as x, y, z, a, b, k, and they represent
real numbers. Vectors are denoted by either a bold-faced lowercase letter, such as u, v, w, or by the
names of the start and end points together with an arrow above. For example, in the xy-plane,
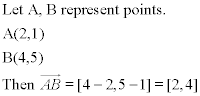
In the above example, the components of the vectors are [2,4]. These were found by subtracting
the x and y values at A from the x and y values at B. If we wanted to call this vector w, we
would write w=[2,4].
Note that vectors are also often shown in column notation, such as 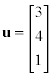 . This
notation is common in the textbook, but its use here will be limited to the examples as it is more
difficult to display in a webpage. . This
notation is common in the textbook, but its use here will be limited to the examples as it is more
difficult to display in a webpage.
The simplest way to understand vectors is to begin with 2-dimensional vectors in the xy-plane.
Let v=[a,b]. In this case, a and b are the components of v. In the xy-plane,
a represents the x component of the vector and b represents the y component. The length
and direction of the vectors are determined by these components. For example, if
we begin at the origin (0,0), then v=[1,2] would be the vector starting at (0,0) and ending at
(1,2). However, two vectors are said to be equivalent (or equal) if their components are the same. Therefore,
a vector u=[1,2] starting at the point (2,4) would end at the point (2 + 1,4 + 2) = (3,6), but is
still equivalent to v. So we can write v=u, since although they lie at different
locations on the xy-plane, their components (and therefore length and direction) are the same.
Vectors can also be interpreted geometrically in the 3-dimensional space xyz. In 3 dimensions, a
vector v=[a,b,c] has 3 components. Similar to 2-dimensional vectors, the components a, b, and c
represent the x, y, and z direction of the vector respectively. For example, beginning again at
the origin (0,0,0), vector v=[4,3,5] would be represented by an arrow starting at (0,0,0) and
ending at (4,3,5). Again, any vector with components [4,3,5] would be considered equal to
v, regardless of where it begins in the xyz space.
Although difficult to interpret geometrically, vectors exist in any n-dimensional space. An n-dimensional
vector has n components. For example, a vector u in Rn (the n-dimensional real number space)
would have components u1, u2, u3, and so on, up to un. Most vector operations are true
for n-dimensional vectors. The exception is the formula for angles between vectors (the answer is true, but the angle
found is only relevant in 2 or 3 dimension vector spaces). As well, two vectors u and v in
Rn are considered equal if and only if their components are equal (uk = vk
for all k = 1...n).
Vector Operations
Vector Length
Sometimes it is necessary to find the length of a vector (also called the norm or magnitude of a
vector.) If we have a vector u=[u1, u2, u3, ..., un],
the length of the vector is found by the formula,
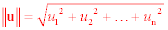
If we have a vector u, the length (or norm, or magnitude) of u is denoted by either
|u| or ||u||. The textbook outlines how the formula for length is
derived from other vector operations. The length of a vector is found as follows:

Addition/Subtraction
Vector addition involves adding the components of the vectors together. Geometrically, this can
be interpreted as adding the vectors 'tip-to-tail.' In order to add two vectors, they must be in the
space with the same number of components (for instance, a two-dimensional vector cannot be added to
a three-dimensional vector). For example, let u=[3,1] and v=[2,5]. To add u + v,
we must add their respective x and y components together,
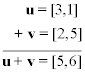
In two and three dimensions, vector addition can be interpreted geometrically. The 'tip-to-tail'
method involves arranging the vectors to be added together by starting each vector at the end of the
previous one (the 'tip' of the first vector is where you place the 'tail' of the next vector.)
The end result can be found by finding the vector that starts at the tail of the first vector, and ends at
the tip of the last vector. For example, let u=[2,1], v=[4,4], and w=[1,3]. The
result is shown below:
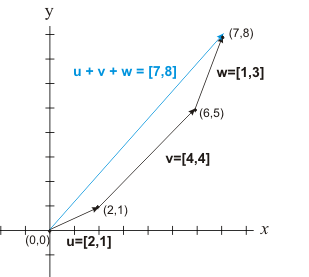
The resulting vector u + v + w=[7,8] is the same as is found by adding the components of the
three vectors together. Similar addition can be performed with 3 dimensional vectors by placing
the vectors tip-to-tail, and finding the vector that runs from the starting point to the end of the last
vector to be added. For example, let u=[3,1,-2] and v=[4,0,3]. By adding components, we
find that u + v = [3 + 4, 1 + 0, (-2) + 3] = [7,1,1].
(Note that in the above example, u had a negative component in the z direction.
Vector components can be any real number, positive or negative.)
When adding vectors in Rn, we can always add them by simply adding their components.
If u=[u1, u2, ..., un] and v=[v1, v2, ..., vn],
then u + v=[u1 + v1, u2 + v2, ..., un + vn]
1
| Find the sum of the vectors in Rn where n>3
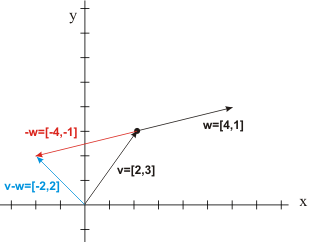
Vector subtraction is simply the negative of addition. Let's start in two dimensions for simplicity's sake.
Let v=[2,3] and w=[4,1]. Then what is v - w? To find v - w, we use the fact
that v - w = v + (-w). Then to find -w, all we have to do is change the sign on all
components of w. So since w=[4,1], -w=[-4,-1], and by adding components, v + (-w)
=[2 + (-4), 3 + (-1)] = [2-4, 3-1] = [-2, 2]. So v - w=[-2, 2]. Geometrically, taking the negative
of a vector makes the vector have the same length, but point in the exact opposite direction. We show the
above example geometrically below,
When taking the negative of a vector, it is very important to change the sign of every component of that
vector. So, if u=[2, -3, 0, 4] in R4, then -u=[-2, 3, 0, -4]. Note that
since the formula for the length of a vector involves squaring each component, then |u| = |-u|. As
with vector addition, the vectors involved must all have the same number of components. Geometric vector
subtraction in 2 or 3 dimensions is still done by the tip-to-tail method, but the vector to be subtracted must be
turned in the opposite direction (which is the equivalent of changing the sign of each component.)
Scalar Multiplication
Multiplication involving vectors is not quite the same as ordinary multiplication involving only scalars. Scalar
multiplication involves multiplying a scalar number by a vector. Let k be a scalar, and u be a vector
in Rn. Since u=[u1, u2, ..., un], then the product
ku=[ku1, ku2, ..., kun]. This is scalar multiplication. Each component
of the vector u is simply multiplied by the scalar k. The result is a vector, and
If k>0, then ku is in the same direction as u, with length k|u|
If k=0, then ku is the zero vector (the starting point is the same, but the length is zero)
If k<0, then ku is in the opposite direction as u, with length |k||u|
We already used scalar multiplication in our look at subtraction, where (-1)u = -u. As
expected, 1u=u. The following table sums up the properties of vector addition/subtraction
and scalar multiplication so far.
1) u + v = v + u
2) u + (v + w) = (u + v) + w
3) u - v = u + (-v)
4) k(u + v) = ku + kv
5) Let a,b be scalars. a(bu) = (ab)u = (ba)u
6) (a + b)u = au + bu
7) |ku| = |k||u|
8) u - u = u + (-u) = 0 (The zero vector)
Note an important fact, that |u + v| ≤ |u| + |v|
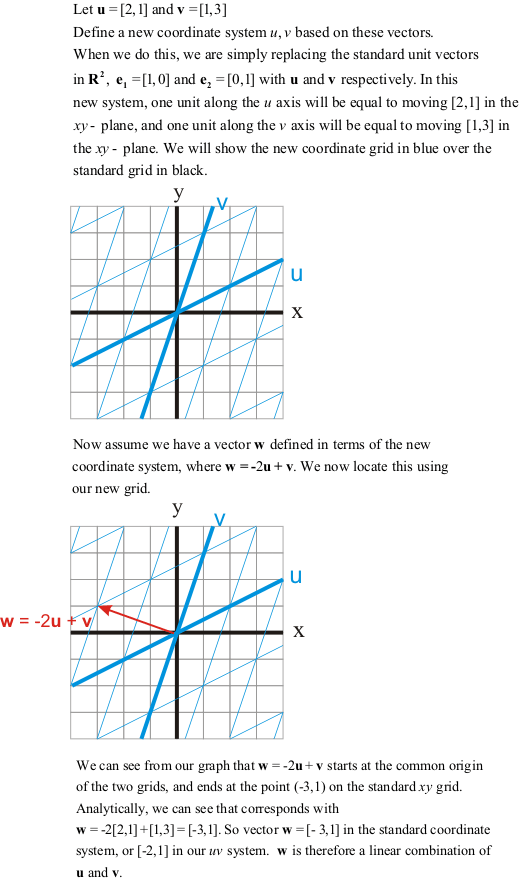
Linear Combinations and Coordinate Axes
Using the concept of scalar multiplication, we can now consider a fact: two vectors u and
v in Rn are parallel if and only if u = kv for some real scalar k. For
example, u=[2,3] is parallel to v=[8,12], since 4u=v, or u=¼v.
Using this fact, we can now discuss linear combinations. If we have a set of vectors v1, v2, ...,
vn, then a vector v is a linear combination of v1, v2, ...,
vn if there is a set of scalars c1, c2, ..., cn (called
coefficients) such that v = c1v1 + c2v2 + ... + cn
vn. For example, u=[2, 5, 7] is a linear combination of v=[1, 3, 2] and
w=[2, 7, 1] since u = 4v - w.
Now let's look at another definition. In an n-dimensional space, the standard unit vectors e
i where i = 1,2,...,n are the vectors with a 1 as the ith component, and zeroes for
all the other components. They are called unit vectors since they have a length of 1. In 2 and 3 dimensions,
these vectors form the basis for the coordinate systems that we use for graphing and interpreting vectors
geometrically. e1, e2 and e3
form the x, y, and (in 3 dimensions) z axes respectively. In R2,
it is possible to form any vector using a linear combination of two non-parallel vectors. We can use
this fact to define new coordinate axes other than e1, e2. This is outlined in
the following example.
The Dot Product
The dot product is a form of multiplication that involves two vectors with the same number of components.
Unlike scalar multiplication, where the result is still a vector, the result of finding the dot product
of two vectors is a scalar (real number). The math involved in finding the dot product is straight forward.
To find the dot product of two vectors, we multiply like components, and find their sum. If we have
vectors u=[u1, u2,...,un] and v=[v1, v2,...,
vn], then the dot product is found by the formula,
u • v = u1v1 + u2v2 +
... + unvn.
The following are properties of the dot product:
1)u • v = v • u
2)u • (v + w) = u • v + u • w
3)cu • v = c(u • v), where c is a scalar
4)u • u ≥ 0, and u • u = 0 if and only if u = 0
5)||v|| = 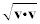
We can use the dot product along with the above properties to derive many important formulas and
concepts in linear algebra. The proofs for many of these are found in the textbook, but here we will look
just at the formulas and examples of their uses.
Normalizing a Vector
Normalizing a vector involves finding a vector that is in the same direction as the original vector,
but whose length is exactly one. Vectors of length one are called unit vectors. The standard
unit vectors shown above are a special case of unit vectors. To find the unit vector, we must
find a scalar to multiply the vector by in order to change its length to 1. To do this, we must find the
length of the vector and multiply the vector by the reciprocal of the length, as follows.

Since normalizing the vector involves scalar multiplication by a positive number, the direction of v is the same as
the direction of u, only the length is changed.
Cauchy-Schwarz Inequality and Triangle Inequality
The dot product allows us to derive two important mathematical inequalities. The proofs are left
to the textbook, but they are listed here:
1) Cauchy-Schwarz Inequality: |u • v| ≤ ||u|| ||v||
2) Triangle Inequality: ||u + v|| ≤ ||u|| + ||v||
We showed the triangle inequality previously as a note regarding vector length, but it is also an
important mathematical inequality that is used elsewhere, and should be remembered. It is easy to see
in the xy plane that this is true (hence the name triangle inequality),
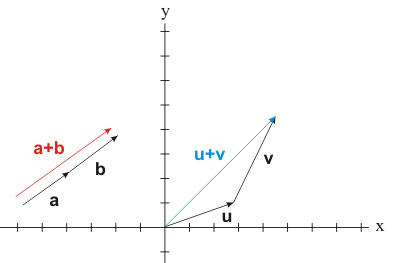
It should be noted that in R2 and R3, the triangle inequality
is only equal if the two vectors are colinear, that is, they lie on exactly the same straight line when
put tip-to-tail (such as vectors a and b in the above picture.)
Distance Between Vectors
We may sometimes be interested to know how far apart two vectors are, when arranged with their tips or tails at
the same point. To do this, we use the formula d(u,v) = ||u - v||. Using this formula, we
are finding the length of the vector that would connect the tails of both vectors. This formula is valid
for all vectors in Rn. Let's look at some examples:
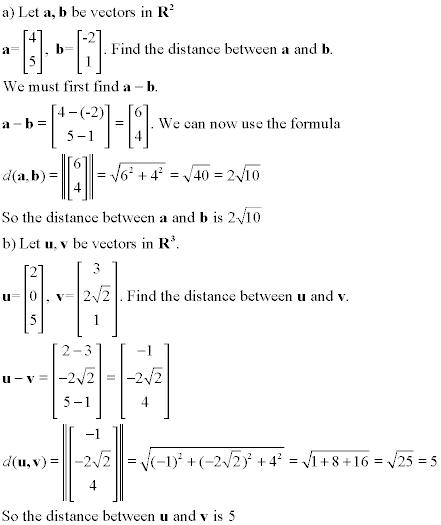
Angle Between Vectors in R2, R3
The dot product also allows us to come up with a convenient formula to find the angle between two vectors.
This formula uses the law of cosines, which is a geometric rule valid in R2 and R3
only, but it can be used as a definition to develop further formulas in Rn

In order to find the exact angle in the above example, we can use the following table for some
common values for cosθ, in order to find the exact degree or radian value for θ.
By remembering that in a right-angle triangle, cosine = (adjacent/hypotenuse), we can use the following
triangles to build the table below.
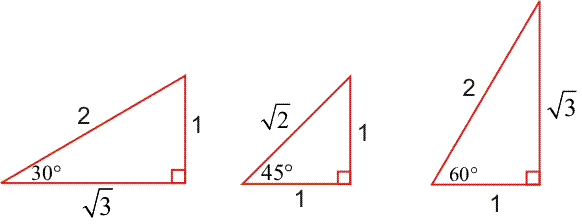

We can now use this table to find the exact angle between vectors u and v in the previous
example,
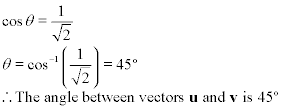
Orthogonality
In the above table, we can see that cosθ = 0 when θ = 90°. From our formula for angle, we
can see that cosθ = 0 if and only if u • v = 0. This gives us the following definition for
orthogonality.
Two vectors u and v are considered to be orthogonal if and only if u • v = 0. This is
denoted by,
u ⊥ v ⇔ u • v = 0
The symbol '⊥' denotes orthogonality. In R2 and R3, orthogonal vectors are equivalent to perpendicular vectors (remember
that perpendicular lines or vectors are at a 90° right angle to one another.) In Rn,
the definition of orthogonality allows us to generalize the idea of perpendicular vectors where our
usual ideas of geometry don't always apply. The following example makes use of our definition of
orthogonal vectors.
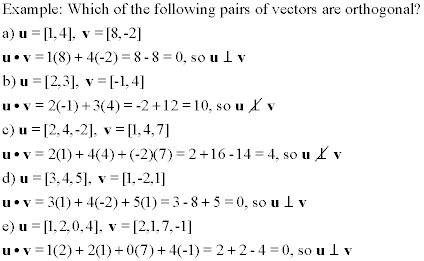
We can use orthogonality to state Pythagoras' Theorem in terms of vector lengths. Given two vectors u and
v, we can say they are orthogonal if and only if ||u + v||2 = ||u||2 + ||v||2, that is
u ⊥ v ⇔ ||u + v||2 = ||u||2 + ||v||2
Vector Projections
The final part of the vector operations section involves using concepts of dot product and orthogonality to
compute vector projections. Given two vectors u and v, the vector projection
(or projection) of v on u is denoted by projuv
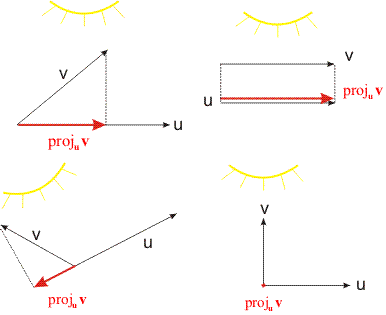
The term projection comes from the idea of shining a light straight down on vector u and seeing
the shadow cast by v on u. This 'shadow' is in the same direction as u, and may have a
different length. Therefore, projuv is a scalar multiple of u. The projection is
found by the formula,
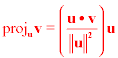
Since the numerator of our scalar is the dot product u • v, we can see that the projection
is the zero vector if u and v are orthogonal. This fits with our analogy, as a perpendicular
vector v would not cast any shadow on u. Similarly, if u = v, then of course
projuv = u, since ||u||2 = u • u, so our scalar would
equal 1. This again fits with our shadow analogy, which is illustrated below,
The component of v on u (or scalar projection) is equal to the length of
the vector projection of v on u. It is denoted compuv, and is given by the
formula,
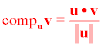
Let's look at a few examples involving projections and components
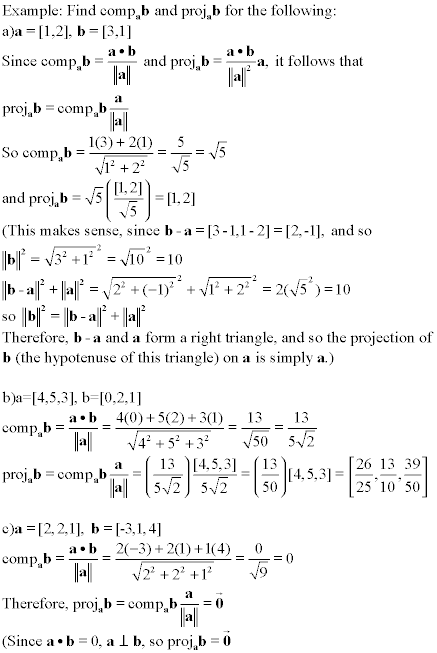
Lines and Planes
Lines in 2 Dimensions
Lines in the xy-plane will be familiar from high school math courses. You will probably be
familiar with one (or both) of the following types of equations for a line,
ax + by = c
y = mx + k, where (rearranging above) m = (-a / b) and k = (c / b), as long as b ≠ 0
(if b = 0, then the line is a vertical line of the form x = c)
When the constants a, b, c (or m, k) are replaced with specific values, this equation describes completely
a line in the xy-plane. A line is the set of all points which satisfy the given equation. Geometrically, this
is a continuous straight line that carrys on forever (unless we specify additional conditions limiting the domain
of the line.) As a refresher, some examples are shown below.
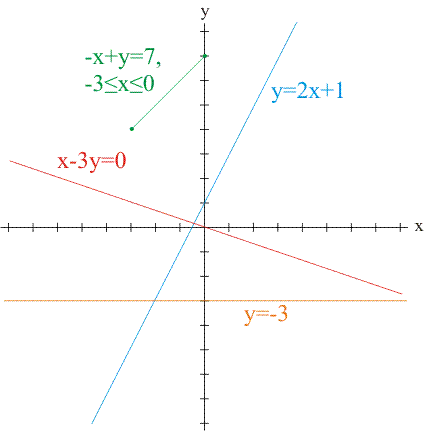
We can now use our knowledge of vectors to describe lines using vector terminology. Given our line in
the form ax + by = c, we define the normal vector to the line to be the vector
n=[a,b]. If we then define a vector x=[x,y], where x is
contains all points (x,y) that satisfy the equation, we can use the
dot product n • x = c to replace the equation of the line.
If c = 0, then the line passes through the origin. In this case, we can see that if n • x
= 0, then n ⊥ x. The normal vector n=[a,b] is therefore perpendicular to our line. If
c ≠ 0, then our normal vector is still perpendicular to the line, since a line with a y-intercept that
is not zero is simply a translation (analogous to a 'slide' on the xy-plane) of a line with the same
slope but passing through the origin.
If we take p to be a vector from the origin to a point on our line l, then we use
this notion to define the normal form of the equation of l as
n • x = n • p
where n=[a,b] is the normal vector and
p=[x0, y0] is any point on our line
The general form of the equation of l is defined as
ax + by = c, where n=[a,b] is the normal vector
Now, define a vector d=[i,j] to be the direction vector of l, that is, a vector that
is parallel to l. (Note that the letters i, j, k are sometimes used to refer
to the x, y, z directions respectively in other math textbooks) To find d, set x = t, set c = 0
and solve the general equation for y. For example,
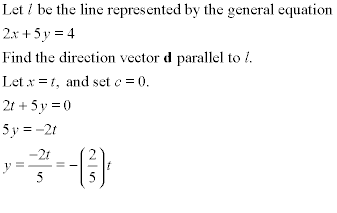
In this example, we see that when x changes by t, then y changes by -(2/5)t. If we divide t out, we
get our direction vector d=[1, (-2/5)], which is parallel to our line 2x + 5y = 4. If we allow
the scalar t to be any real number, we can make td carry on forever, which a line does unless
we restrict its domain. Now all that is needed to use vectors to completely define a line is to move
this vector td to the proper position in the xy-plane so that the y-intercept is where
it should be. To do this, we define p to be any point on our line l. We can now define the
vector form of the equation of l.
x = p + td
where p=[x0, y0] is any fixed point on l
Now let's finish our example,
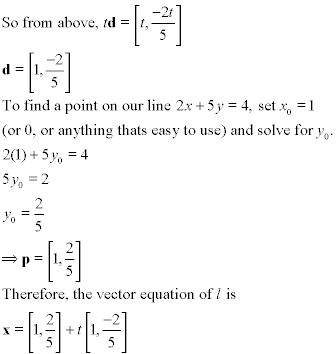
We have now completely defined l in terms of vectors. This is extremely useful in linear
algebra, and in many other mathematical applications such as vector calculus. We can use this to
come up with another definition, the parametric equations of l. These are defined as
the componentwise equations corresponding to the vector equation, so if x = p + td is
the vector equation, then
x = x0 + (i)t
y = y0 + (j)t
are the parametric equations of l
Please notice that there are infinitely many possiblities for vector and parametric equations for
the same line, since we can take any point for p and use any scalar multiple of d. Let's
look at a couple of additional examples before moving on to lines and planes in R3.
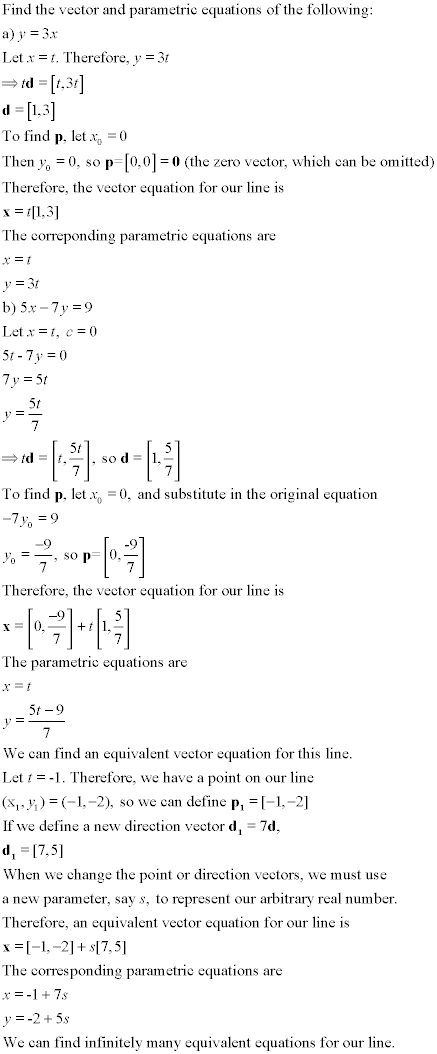
2
| Find the equation of the line using projections
Lines and Planes in 3 Dimensions
You might think that a single equation such as ax + by + cz = d would be the general equation of
a line in 3 dimensions. However, such an equation defines a plane in R3, which
geometrically is a flat surface which carrys on forever in the space. This is explained by our normal
form for the equation of a line, where n • x = n • p. In 3 dimensions, a vector has
infinitely many orthogonal vectors, which sweep out around it forming a plane, whereas in 2 dimensions
the orthogonal vector is unique and forms a line.
So how is a line defined in 3 dimensions? We have a couple of options. We can use two equations of
the form ax + by + cz = d, (or two normal form equations) which would define two planes, and then find the line where those two planes
intersect. This requires knowledge from the next section on solving systems, and is quite tedious in
most situations. Our vector and parametric equations, however, are easy to generalize to three dimensions.
To define a line in 3 dimensions, we simply need to add a third component to the vector equation (or
a corresponding third parametric equation.) Let's look at some examples.

From the above example, it can be seen how 3 dimension vector and parametric equations for a line are
as easy to use as they were for 2 dimensions. The vector form of the equation for a line allows us
to use a single equation to describe a line in 2 or 3 dimensions, rather than needing one general equation
for a 2 dimension line or two general equations for a line in 3 dimensions.
As mentioned above, a single general equation of the form ax + by + cz = d describes a plane in the
three dimensional space. In addition, the vector n=[a,b,c] represents the normal vector of the plane,
that is, a vector which is orthogonal to the entire plane. The scalar value d is similar to the y-intercept
of a line; it defines where the plane is located.
Similarly, the normal form for the equation of a plane is defined by the single equation
n • x = n • p, where n=[a,b,c] is the normal vector orthogonal to the plane, and
p is a vector from the origin to a point on the plane.
We can also define a plane using vector and parametric equations. In order to do this, we need a vector p
to a point on the plane, and two nonparallel direction vectors u and v. By having
two direction vectors, we can find all points on the plane by using all scalar multiples su and
tv, similar to the vector equation of a line. The parametric equations are again just the
componentwise equations that make up the vector equation. Let's look at some more examples.

Distance between a Point and a Line or Plane
We have easy to use formulas to find the distance from a given point to a line or a plane. They are based on the
idea of vector projections, and a more detailed explanation is given in the textbook. Here, we will give
the formulas, and a few examples of their use.
Given a line l and a point A(x0,y0,z0) in two dimensions (on
the plane, xy-plane or otherwise), the distance from A to the line is given by the formula,
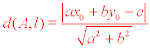
where l is given by the general equation ax + by = c
Given a plane P and a point A(x0,y0,z0), the distance from
the point A to the plane is given by the formula,
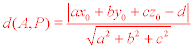
where P is given by the general equation ax + by + cz = d
Let's look at a couple of examples:
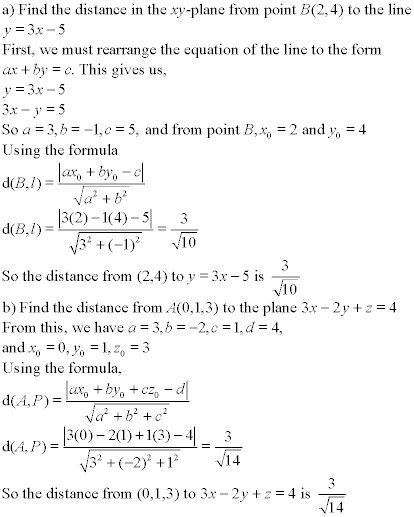
The Cross Product
The final part of this tutorial is a special vector operation called the cross product. The
cross product is only valid in R3, and it gives us a vector orthogonal to any two
nonparallel vectors. Given vectors u=[u1,u2,u3] and
v=[v1,v2,v3], the cross product u × v = [(u2v3
- u3v2), (u3v1 - u1v3), (u1v2
- u2v1)]. This is a pretty complicated formula to try and remember, but there are a couple
of tricks that you can use. You may notice that in the first bracket, there are no subscript 1's, in the
second, no 2's, and in the third, no 3's. Another, more visual, way to remember is to write out
the components of the vectors as follows (this method is also shown in the textbook),
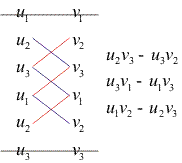
If you write out the two vectors in columns twice side by side as shown above, you first cross
out the top and bottom pairs. Then, add products from the top-to-bottom diagonals shown in blue, and
subtract products from the bottom-to-top products shown in red.
The cross product formula is complicated, but important to memorize it for this and other math
courses. Once we're familiar with matrices and determinants, there is another method for finding the cross product,
but we'll leave it for now, since we haven't seen determinants yet.
Please note that u × v = - (v × u). It's also important to remember that while the dot product gives us a scalar, the cross product
gives us another vector in R3.
We end with some examples of the cross product.

3
| Find the general equation of the plane
|
Top of Page |
|

