Orthogonal Sets
Vectors v, u are orthogonal or
perpendicular to each other if v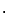 u = 0 whenever v
u = 0 whenever v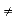 u. We say a set of vectors
{v1, v2, ... , vk}
is an orthogonal set if for all vj and vi,
vj u. We say a set of vectors
{v1, v2, ... , vk}
is an orthogonal set if for all vj and vi,
vj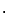 vi = 0
where i vi = 0
where i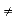 j and i, j = 1, 2, ... , k j and i, j = 1, 2, ... , k
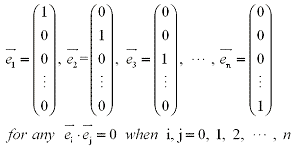
We can show easily that the standard basis in  is an
orthogonal set is an
orthogonal set
This is also true for any subset of the standard basis. Example one checks some other
vectors for orthogonality.
Next we will look at some theorems that apply to orthogonal sets.
Theorem 1:
If we have an orthogonal set {v1,
v2, ... , vk}
in  then vectors v1, v2,
... , vk are all linearly independent.
then vectors v1, v2,
... , vk are all linearly independent.
1
| Proof
Theorem 2:
An orthogonal set of vectors
v1, v2, ... , vn
in  form an orthogonal basis of form an orthogonal basis of 
Theorem 3:
Letting {v1, v2, ... , vk}
be an orthogonal basis for a subspace of  and let w be any vector in the
subspace and let w be any vector in the
subspace  .
Then there exists scalars c1, c2, ... , ci, ... ,
ck such that: .
Then there exists scalars c1, c2, ... , ci, ... ,
ck such that:
w = c1v1+c2v2+
... + civi+ ... +ckvk
Examples:
1
| Check vectors for orthogonality
2
| Find coordinates with respect to a basis
Orthonormal Sets
Next we will begin to explain the difference between an orthogonal and an
orthonormal set.
The length or magnitude
of v in  is defined as ||v|| = is defined as ||v|| = 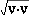
A unit vector u in  is a vector that has a length or
magnitude of one. In other words: ||u|| = 1 or u is a vector that has a length or
magnitude of one. In other words: ||u|| = 1 or u u = 1 u = 1
An orthonormal set is a set of vectors
{v1, v2, ... , vk}
which is orthogonal and every vector in the set is a unit vector. In other words for every vector vi in the set:
||vi|| = 1 and 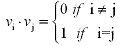
where i = 1, 2, ... , k
It is quick and easy to obtain an orthonormal set for vectors from an orthogonal set of vectors, simply divide
each vector by its length.
Theorem 4:
If {v1, v2, ... , vk}
is an orthonormal basis of a subspace of  then for any vector w in the
subspace, w can be expressed as: then for any vector w in the
subspace, w can be expressed as: w = (w v1)v1+
(w
v1)v1+
(w v2)
v2+ ... +
(w v2)
v2+ ... +
(w vk)
vk vk)
vk
Orthogonal Matrices
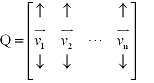 An orthogonal matrix is simply a matrix whose columns are made up vectors form an orthogonal set.
Letting Q be an orthogonal matrix we can then say that
v1, v2, ... , vn
(the columns of Q) form an orthongal set. Several theorems related to orthogonal matrices
working with finding and maniputlating the transpose of the matrix. Therefore before getting into the theorems
it would be benifical to first look at the properties of the transpose
An orthogonal matrix is simply a matrix whose columns are made up vectors form an orthogonal set.
Letting Q be an orthogonal matrix we can then say that
v1, v2, ... , vn
(the columns of Q) form an orthongal set. Several theorems related to orthogonal matrices
working with finding and maniputlating the transpose of the matrix. Therefore before getting into the theorems
it would be benifical to first look at the properties of the transpose
Properties of the Transpose
1. If A is an n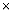 m matrix and B is an
m m matrix and B is an
m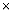 p matrix then (AB)T =
BTAT p matrix then (AB)T =
BTAT
2. If an n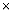 n matrix A is invertible then so is
AT and (AT)-1
= (A-1)T n matrix A is invertible then so is
AT and (AT)-1
= (A-1)T
Theorem 5:
Let Q be and n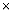 n matrix. Then Q is orthogonal if and only if
QTQ = In
or equallently Q-1 = QT n matrix. Then Q is orthogonal if and only if
QTQ = In
or equallently Q-1 = QT
5
| Proof
Theorem 6:
Consider an n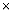 n matrix. Then Q then the following
statements are equivallent: n matrix. Then Q then the following
statements are equivallent:
1. Q is an orthogonal matrix
2. Q-1 = QT
3. QTQ = In
4. Qx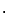 Qy = x Qy = x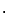 y for all
x, y that exists in y for all
x, y that exists in 
5. ||Qx|| = ||x|| which means, Q preserves length for every x in

6
| Proof
Theorem 7:
If Q is orthogonal then its rows form an orthonormal set of vectors and the columns of
QT form an orthonormal set.
7
| Proof
Examples:
3
| Check if a matrix is orthogonal
Orthogonal Complements
The definition of orthogonal complement is similar to that of a normal vector. A
vector n is said to be normal to a plane if it is orthogonal to every vector in that plane.
Letting W be a subspace of  and v be a vector
in and v be a vector
in  then v is considered orthogonal to W
if v is orthogonal to every vector that is contained in W. The orthogonal
complement of W is the set of all vectors that are orthogonal to W.
We will denote this set as W then v is considered orthogonal to W
if v is orthogonal to every vector that is contained in W. The orthogonal
complement of W is the set of all vectors that are orthogonal to W.
We will denote this set as W  pronounced the W perp.
pronounced the W perp. W  =
{v in =
{v in  : v : v 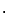 w = 0 for all w in W}
w = 0 for all w in W}
Theorem 8:
Let W be a subspace of 
1. W  is a subspace of is a subspace of 
2. (W  ) )
 = W = W
3. W 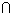 W W  =
{0} =
{0}
8
| Proof
Theorem 9:
Let A be an m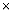 n matrix.
Then n matrix.
Then (row(A)) =
null(A) and (col(A)) =
null(A) and (col(A)) =
null(AT) =
null(AT)
See the proof for a more detailed explaintion of this theorem.
9
| Proof
From this we see that a m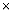 n
matrix A has four fundamental subspaces. The row(A),
and the null(A) are the orthogonal complement in n
matrix A has four fundamental subspaces. The row(A),
and the null(A) are the orthogonal complement in  and the col(A), and the null(AT)
are the orthogonal complement in
and the col(A), and the null(AT)
are the orthogonal complement in 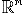 . .
Examples
4
| Find the orthogonal complement of a subspace
Orthogonal Projections
The definition of the projection of a vector v onto a onto a nonzero vector u
was given in previous lectures by:
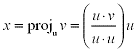
Now consider a subspace W of  with
an orthogonal basis u1, u2
, ... , uk. Let v be any vector in with
an orthogonal basis u1, u2
, ... , uk. Let v be any vector in
 , then the orthogonal projection of v onto
W is defined as: , then the orthogonal projection of v onto
W is defined as:
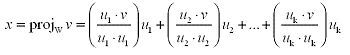
If you have an orthonormal basis w1,w2, ... ,
wk of a subspace W and v is any vector in
 then the orthonormal projection of v onto W
is defined as: then the orthonormal projection of v onto W
is defined as:
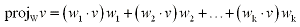
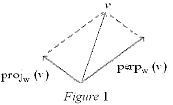 Since the projw(v) is the projection of
the vector v onto the subspace W we can also find a vector which is perpendicular
or orthogonal to this projection. This vector is called
perpw(v).
We can decompose v as: Since the projw(v) is the projection of
the vector v onto the subspace W we can also find a vector which is perpendicular
or orthogonal to this projection. This vector is called
perpw(v).
We can decompose v as:
v = projw
(v) + perpw(v)
The next theorem explains that you can always decompose a vector with respect to a subspace
and its orthogonal complement.
Orthogonal Decomposition Theorem:
Let a vector v and a subspace W exist in  .
Then there exists a unique vector w in W and w .
Then there exists a unique vector w in W and w  in W
in W  such that: such that: v = w +
w 
Theorem 11:
If W is a subspace of  ,
then ,
then dim W + dim W  =
n =
n
11
| Proof
Rank Nullity Theorem:
If A is an m n matrix,
then n matrix,
then rank(A) + nullity(A)
12
| Proof
Examples
5
| Find the orthogonal projection
The Gram-Schmidt Process
As shown in the earlier examples, sometimes it is useful to have an orthogonal or
orthonormal basis of a subspace of  .
There is a simple algorithm for constructing such a thing call the Gram-Schmidt Process. .
There is a simple algorithm for constructing such a thing call the Gram-Schmidt Process.
If we had a subspace W of  that has a
two dimentional basis, x1 and x2
and we want to find an orthogonal basis w1 and w2
we use the Gram-Schmidt Process: that has a
two dimentional basis, x1 and x2
and we want to find an orthogonal basis w1 and w2
we use the Gram-Schmidt Process:
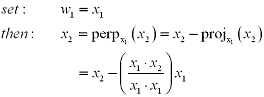
If you have a subspace W in  where W has a larger basis x1, x2,
... , xk follow the steps outlined in the algorithm in order to
construct an orthogonal basis w1, w2,
... ,wk of W.
where W has a larger basis x1, x2,
... , xk follow the steps outlined in the algorithm in order to
construct an orthogonal basis w1, w2,
... ,wk of W.
Algorithm:
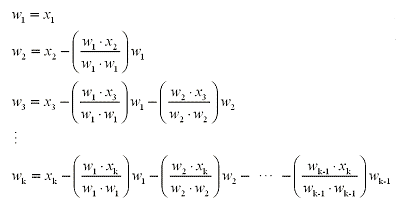
Examples
6
| Find an orthogonal basis for the subspace
The QR Factorization
QR Factorization is a way of using the Gram-Schmidt Process to factor a m n
matrix M with linearly independent columns. This factorization proves to be very useful
to many other topics we will cover. n
matrix M with linearly independent columns. This factorization proves to be very useful
to many other topics we will cover.
The QR Factorization Theorem:
Consider an m n matrix M with linearly independent
columns. Then M can be factored as M = QR, where Q is an
m n matrix M with linearly independent
columns. Then M can be factored as M = QR, where Q is an
m n matrix whose columns are orthonormal and R
which is an invertible upper triangular matrix. n matrix whose columns are orthonormal and R
which is an invertible upper triangular matrix.
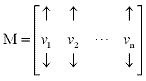 Using QR Factorization is easy. Take an m
Using QR Factorization is easy. Take an m n matrix
M with linearly independent columns v1,
v2, ... , vn. Then by using the
Gram-Schmidt Process on the columns of M, find the orthonormal columns n matrix
M with linearly independent columns v1,
v2, ... , vn. Then by using the
Gram-Schmidt Process on the columns of M, find the orthonormal columns
w1, w2, ... ,
wn of Q.
Now each column vector v1,
v2, ... , vn
in M can be factored using the column vectors in Q.
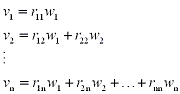
The scalars r1i, r2i, ... ,rii
(where i = 1, 2, ... , n) make up R. Then M can be broken down in the following QR Factorization.
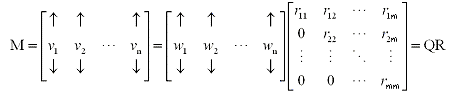
And the following method can be used to find each scalar in R:
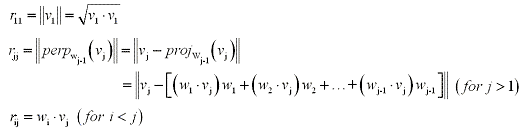
Note: In the above method, wi where i = 1, 2, ... , n must be
orthonormal vectors, not orthogonal.
Examples
7
| Find the QR Factorization of the matrix
NOTE: This website has
been designed for and tested for functionality on Internet Explorer
6.0, Netscape Navigator 7.2, Netscape Browser 8.0,
and
Mozilla Firefox 1.0. Other browsers may not display information
correctly, although future versions of the abovementioned browsers
should function properly.
|

