|
This tutorial includes many theorems that involve vector spaces and other topics that
apply to vector spaces. To gain the best understanding of the material covered it is
suggested that you review each proof or if there is none, try to prove each theorem on your
own. Also each topic has several examples that pertain to the theorems or definitions given
and should also be reviewed.
Vector Spaces
If we have a set V and u and v exist in V
then V is said to be closed under addition if u + v exists in V
If v is in V, and k is any scalar, then V is said to be closed under
scalar multiplication if kv exists in V
A vector space or linear space V, is a set which satisfies the
following for all u, v and w in V and scalars c and d:

Probably the most improtant example of a vector space is 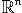 for any n
for any n  1. We can easily see that the additive identity 0
exists and it is closed under addition and scalar multiplication. To show that 1. We can easily see that the additive identity 0
exists and it is closed under addition and scalar multiplication. To show that 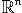 satisfies the other 8 properties very simple and
is left as an exercise. satisfies the other 8 properties very simple and
is left as an exercise.
The examples given at the end of the vector space section examine some vector spaces more
closely. To have a better understanding of a vector space be sure to look at each example listed.
Theorem 1:
Let V be a vector space, u a vector in V and c a scalar then:
1) 0u = 0
2) c0 = 0
3) (-1)u = -u
4) If cu = 0, then c = 0 or u = 0
Examples:
1
| Show if a set is a vector space
2
| 3 Examples of a vector spaces
Subspaces
A subset W of a linear space V is called a subspace
of V if:
1) W contains the additive identity 0
2) W is closed under addition
3) W is closed under scalar multiplication
Basically a subset W of a vector space V is a subspace if
W itself is a vector space under the same scalars and addition and scalar
multiplication as V.
Consider the set of vectors S={v1,
v2, ... , vk} of a vector
space V. Then we say the span of v1,
v2, ... , vk is the set
of all linear combinations of v1,
v2, ... , vk and is
denoted span(S). If V = span(S) then S is called a spanning set for
V and V is spanned by S.
Theorem 2:
Let v1, v2, ... ,
vk be vectors in a vector space V then:
1) span(v1, v2, ... ,
vk) is a subspace of V
2) span(v1, v2, ... ,
vk) is the smallest subspace of V that
contains v1, v2, ... ,
vk
Examples:
3
| Show that a set is a subspace
Linear Independance
We have covered what linear independance is in previous tutorials but will now apply it
to vector spaces.
We say a set of vectors v1,
v2, ... , vk are linearly
independent if the equation:
c1v1+
c2v2+...+
ckvk = 0
only has trivial solution: c1 =
c2 = ... = ck = 0
If a set is not linear independent then it is said to be linearly dependent. This
means that there is at least one ci in the above equation
such that ci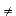 0 where i = 1, 2, ... , k.
0 where i = 1, 2, ... , k.
Theorem 3:
A vector set {v1, v2,
... , vk} in a vector space V is linearly
dependent if and only if at least one vi (where i = 1, 2,
... , k) can be written as the linear combination of the others.
We say that elements v1, v2,
... , vk form a basis of a vector space
V if they span V and are linearly independent. This means that
all v in V can be written uniquely as a
linear combination ie: v =
c1v1+
c2v2+ ... +
ckvk
The scalars or coefficients c1,
c2, ... , ck are called
the coordinates of v with respect to the basis  =
{v1,
v2, ... , vk} and the column
vector: =
{v1,
v2, ... , vk} and the column
vector:
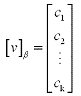
is called the coordinate vector of v with respect to

Theorem 4:
Consider a basis  for a subspace V and let
u , v be vectors in V and c a scalar. Then: for a subspace V and let
u , v be vectors in V and c a scalar. Then:
1) [u + v]B =
[u]B + [v]B
2) [cu]B = c[u]B
4
| Proof
Theorem 5:
Let V be a vector space with a basis  =
{v1,
v2, ... , vk} and
u1, u2, ... ,
uk be vectors in V. Then the set
{u1, u2, ... ,
uk} is linearly independent in V if and only
if =
{v1,
v2, ... , vk} and
u1, u2, ... ,
uk be vectors in V. Then the set
{u1, u2, ... ,
uk} is linearly independent in V if and only
if
{[u1]B,
[u2]B, ... ,
[uk]B} is linearly independent
in 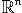 . .
Examples:
4
| Find the basis
Dimention
The dimention of a subspace V or dim(V) is the number
of vectors in the basis of V. Finite-dimentional defines a basis which
has a finite number of vectors and infinite-dimentional defines a basis which has
infinite number.
Theorem 6:
If a subspace V has a basis  =
{v1, v2, ... ,
vk} then: =
{v1, v2, ... ,
vk} then:
1) Any set of more then k vectors in V must be linearly dependent
2) Any set of fewer then k vectors in V cannot span V
3) Every basis for V has exactly k vectors
6
| Proof
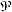 is the set of all polynomials and has a basis:
{1, x, x2, ... }. Since the basis has an infinte number of elements then is the set of all polynomials and has a basis:
{1, x, x2, ... }. Since the basis has an infinte number of elements then
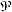 has infinte dimention. has infinte dimention. 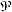 n on the other hand contains n + 1 vectors in the basis, therefore is finite-dimentional
n on the other hand contains n + 1 vectors in the basis, therefore is finite-dimentional
Theorem 7:
If W is a subspace of a finite dimentional vector space V then:
1) W is finite dimentional and dim(W)
 dim(V) dim(V)
2) dim(W) = dim(V) if and only if W = V
Examples:
5
| Find a basis and determine the dimention
Change of Basis
If we had two bases  =
{u1, u2, ... ,
un
and =
{u1, u2, ... ,
un
and 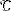 = {v1,
v2, ... ,vn}
for a vector space V then there is a n = {v1,
v2, ... ,vn}
for a vector space V then there is a n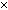 n
matrix whose columns are the coordinate vectors
[u1]C,
[u2]C, ... ,
[un]C of the vectors in n
matrix whose columns are the coordinate vectors
[u1]C,
[u2]C, ... ,
[un]C of the vectors in
 with respect to with respect to 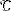 is called the change-of-basis matrix from
is called the change-of-basis matrix from  to to
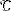 . It is denoted by . It is denoted by 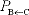 That is:
That is:
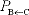 =
[[u1]C,
[u2]C, ... ,
[un]C] =
[[u1]C,
[u2]C, ... ,
[un]C]
This may seem complicated, but simplily put the columns of 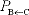 are just the corrdinate vectors obtained by writing the "old basis
are just the corrdinate vectors obtained by writing the "old basis  in terms of the new basis
in terms of the new basis 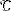 . Try some of the examples
in order to see how this is applied. . Try some of the examples
in order to see how this is applied.
Theorem 8:
If we had two bases  and and 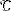 for a vecor space V and change-of-basis
for a vecor space V and change-of-basis 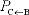 then:
then:
1) 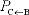 [x]B =
[x]C for all x in V. [x]B =
[x]C for all x in V.
2) 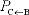 is the unique matrix P with the
property that P[x]B = [x]C
for all x in V. is the unique matrix P with the
property that P[x]B = [x]C
for all x in V.
3) 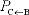 is invertible and
( is invertible and
(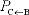 )-1 = )-1 = 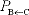
8
| Proof
Gauss-Jordan elimination is regularily used to find the inverse of a matrix. Finding the
change-of-basis matrix from a standard basis requires the calculation of a matrix inverse.
Therefore with a slight modification we can use the Gauss-Jordan method to find the change-of-basis
matrix between two nonstandard bases. The following theorem explains how.
Theorem 9:
Consider a subspace V with bases
 ={u1,
u2, ... , un} and ={u1,
u2, ... , un} and
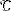 ={v1,
v2, ... , vn}. If
B = [[u1]E,
[u2]E, ... ,
[un]E] and
C = [[v1]E,
[v2]E, ... ,
[vn]E] where ={v1,
v2, ... , vn}. If
B = [[u1]E,
[u2]E, ... ,
[un]E] and
C = [[v1]E,
[v2]E, ... ,
[vn]E] where
 is any
basis for V then row reduction applied to [ C | B ] produces: is any
basis for V then row reduction applied to [ C | B ] produces:
[ C | B ] [ I |
[ I | 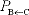 ] ]
Examples:
6
| Find the change-of-basis matrix
Linear Transformations
Consider two vector spaces V and W a function or mapping
T from V to W is called a linear transformation if for
all u, v in V and all scalars k:
1) T(u + v) = T(u) + T(v)
2) T(ku) = kT(u)
A mapping T:V to W is also a linear transformation if and
only if for all v1, v2,
... ,vn in V and scalars
c1, c2, ... ,
cn T(c1
v1 + c2
v2 + ... + cn
vn) = c1T(
v1) + c2T(
v2) + ... + cnT(
vn)
Theorem 10:
If T is a linear transformation from V to W and
u and v exist in V then:
1) T(0) = 0
2) T(-v) = -T(v)
3) T(u - v) = T(u) - T(v)
10
| Proof
Theorem 11:
Consider a linear transformation T from V to W letting
 = {v1,
v2, ... , vn}
be a spanning set for V. Then T( = {v1,
v2, ... , vn}
be a spanning set for V. Then T( ) =
{T(v1), T(v2), ... ,
T(vn)} spans the range of T. ) =
{T(v1), T(v2), ... ,
T(vn)} spans the range of T.
11
| Proof
Examples:
7
| Show whether a transformation is linear
8
| Show whether a transformation is linear
Composition of a Linear Transformations
The compostion of a linear transformation is similar to the composition of a
function in calculus.
If T is a linear transformation from U to V and S is a linear
transformation from V to W then the composition of S with T is
the transformation or mapping S T
defined by T
defined by S T(u) =
S(T(u) where u exists in U T(u) =
S(T(u) where u exists in U
The next theorem follows directly from the definition:
Theorem 12:
If T from U to V and S from V to W
are linear transformation then S T from
U to W is a linear transformation. T from
U to W is a linear transformation.
A linear transformation T from V to W is invertible
if there exists a linear transformation T' from W to V
such that T' T = I
V and T T = I
V and T T' =
IW T' =
IW
Properties of inverses: If T is a linear transformation from V to
U then:
1) If T is invertible then so is T'
2) If T is invertible then it's inverse is unique
3) T is invertible if and only if ker(T)={0} and im(T)=W
Examples:
9
| Show whether a transformation is invertible
Kernel and Range of a Linear Transformation
Consider a linear transformation T that goes from V to W. Then
the kernel of T or the ker(T), is the set of all vectors which takes T to 0 or the
null set in W. This can be shown in the following:
ker(T) = {v in V: T(v) = 0}
Another useful definition in this unit is the range of T, also refered to as the image of T and is
denoted range(T). It is similar to the range of a function in calculus in that it is the set
of all vectors in W which are images of the vectors
in V under T. This can be shown in the following:
range(T) = {w in W: w = T(v for some v in W)
Theorem 13: The Rank-Nullity Theorem
Consider the linear transformation T from V to W where V and W
are finite dimentional then:
nullity(T) = dim(ker(T)) and rank(T) = dim(range(T))
Then:
rank(T) + nullity(T) = dim(V)
13
| Proof
Examples:
10
| Find the image and kernel of the transformation
One-to-One and Onto Linear Transformations
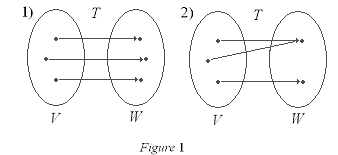
Consider a linear transformation T from V to W. T is said
to be one-to-one if for all u and v in V:
u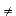 v v 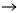 T(u)
T(u) 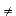 T(v) T(v)
and
T(u) = T(v) 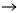 u = v
u = v
Figure 1 shows two examples of one-to-one functions. Both are also onto (see the next definition).
A linear transformation T from V to W is said to be onto
if for all w and W there is at least one v in V such that::
w = T(v)
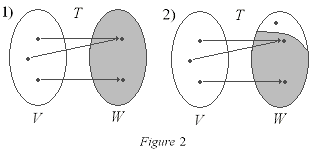
Figure 2 has two examples. the first is onto beacause every point in W exists in V.
The second example is not onto, beacause there is one point in W which does not corresponded to
a point in V by T.
The following theorems can be used to solve various problems dealing with linear transformations.
Before trying to manipulate the theorems it maybe better to view each proof first to gain
a better understanding of each theorem.
Theorem 14:
A linear transformation is one-to-one if and only if ker(T)={0}
14
| Proof
Theorem 15:
Let dim(V) = dim(W) = n. Then a linear transformation T from
V W is one-to-one
if and only if is onto W is one-to-one
if and only if is onto
15
| Proof
Theorem 16:
Consider a one-to-one linear transformation T from
V W. Then if we have a
linearly independent set S={v1, v2, ... ,
vk} then T(S)={T(v1),
T(v2), ... , T(vk)} is
also linearly independent in W. W. Then if we have a
linearly independent set S={v1, v2, ... ,
vk} then T(S)={T(v1),
T(v2), ... , T(vk)} is
also linearly independent in W.
16
| Proof
Theorem 17:
A linear transformation is invertible if and only if it is both one-to-one and onto
17
| Proof
Examples:
11
| Find if the linear transformation is one-to-one and onto
12
| Show that the transformation is invertible
Isomorphisms of Vector Spaces
An invertible linear transformation is called an isomorphism. We say that the linear
spaces V and W are isomorphic if there is an isomorphism from
V to W.
Properties of isomorphisms:
Consider a linear transformation T from V to W
1) If T is an isomorphism, the so is T-1
2) T is an isomorphism if and only if ker(T) = {0} and range(T) = W
3) If v1, v2, ... ,
vk is a basis in V then
T(v1), T(v2), ... ,
T(vk) is a basis in W
4) If V and W are finite dimentional vector spaces, then
V is isomorphic to W if and only if
dim(V) = dim(W)
Examples:
13
| Show that the transformation is an isomorphism
Matrix of a Linear Transformation
Consider a linear transformation T from  to to
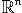 and a basis and a basis  of of
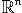 . The n . The n n matrix
B that transforms [x]B into
[T(x)]B is called the n matrix
B that transforms [x]B into
[T(x)]B is called the  -matrix
of T for instance for all x in -matrix
of T for instance for all x in 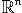 : :
[T(x)]B = B[(x)]B
Constructing a  -matrix B of a linear transformation T
column by column is easy. If we had a vector x in -matrix B of a linear transformation T
column by column is easy. If we had a vector x in 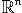 such
that: such
that:
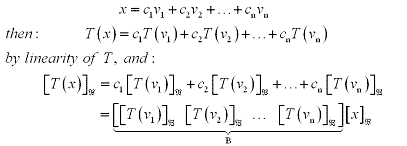
Consider a linear transformation T from 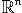 to to
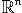 and a basis and a basis  of
of 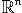 consisting of vectors v1,
v2, ... , vn. Then the
columns of B are the consisting of vectors v1,
v2, ... , vn. Then the
columns of B are the  -coordinate vectors of
T(v1), T(v2), ... ,
T(vn). Then the -coordinate vectors of
T(v1), T(v2), ... ,
T(vn). Then the  -matrix
of T is: -matrix
of T is:
B=[[T(v1)]B,
[T(v2)]B, ... ,
[T(vn)]B]
To clear things up a bit look at the following diagram. Say we had a basis
 of a subspace V of of a subspace V of
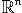 , consisting of vectors v1,
v2, ... , vm. Then any
vector x in V can be written uniquely as : , consisting of vectors v1,
v2, ... , vm. Then any
vector x in V can be written uniquely as :
x = c1v1,
c2v2, ... ,
cmvm
the scalars are called the  -coordinates of x and
the -coordinates of x and
the  -coordinate vector of x denoted by
[x]B is would be: -coordinate vector of x denoted by
[x]B is would be:

Note that:
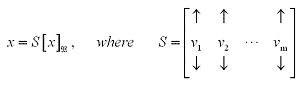
Then our diagram looks like this:
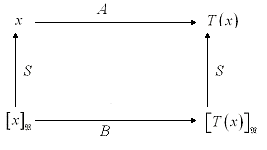 where T(x) = A(S[x]B) and also T(x) =
S(B[x]B) so that A(S[x]B) =
S(B[x]B) for all x. Thus:
where T(x) = A(S[x]B) and also T(x) =
S(B[x]B) so that A(S[x]B) =
S(B[x]B) for all x. Thus:
AS = SB, B = S-1AS and A = SBS-1
Consider two n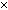 n matrices A and B. We say that A is
similar to B if there is an invertible matrix S such that: n matrices A and B. We say that A is
similar to B if there is an invertible matrix S such that:
AS = SB or B = S-1AS
Similarity relations:
1) An n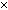 n matirx A is simlar to itself (REFLEXIVE) n matirx A is simlar to itself (REFLEXIVE)
2) If A is similar to B then B is similar to A (SYMMETRY)
3) If A is similar to B and B is similar to C then A is similar to C (TRANSITIVITY)
Theorem 18: The Fundamental Theorem of Invertible Matrices:
Let T be a linear transformation from V to W and A be an
n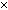 n matrix such that T(x) = Ax for any
x in V. Then the following statements are equivalent: n matrix such that T(x) = Ax for any
x in V. Then the following statements are equivalent:

Examples:
14
| Find the matrix of the transformation
15
| Three part question
NOTE: This website has
been designed for and tested for functionality on Internet Explorer
6.0, Netscape Navigator 7.2, Netscape Browser 8.0,
and
Mozilla Firefox 1.0. Other browsers may not display information
correctly, although future versions of the abovementioned browsers
should function properly.
|

