Complex Numbers
A complex number is made up of both real and imaginary components. It can be
represented by an expression of the form (a+bi), where a and b are real numbers and i is imaginary.
When defining i we say that i = 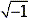 .
Then we can think of i2 as -1. In general, if c is any positive number, we would write: .
Then we can think of i2 as -1. In general, if c is any positive number, we would write:
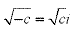 . .
If we have a complex number z, where z=a+bi then a would be the real 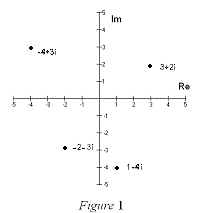 component (denoted: Re z) and b would represent
the imaginary component of z (denoted Im z). Thus the
real component of z=4+3i
is 4 and the imaginary component would be 3. From this, it is obvious that two
complex numbers (a+bi) and (c+di)
are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.
component (denoted: Re z) and b would represent
the imaginary component of z (denoted Im z). Thus the
real component of z=4+3i
is 4 and the imaginary component would be 3. From this, it is obvious that two
complex numbers (a+bi) and (c+di)
are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.
The complex number (a+bi) can also be represented by the ordered pair (a,b) and
plotted on a special plane called the complex plane or the Argand Plane. On the
Argand Plane the horizontal axis is called the real axis and the vertical axis is
called the imaginary axis. This is shown in Figure 1 on the right:
Properties of the Complex Set
The set of complex numbers is denoted 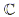 . Just like any other number set there
are rules of operation. . Just like any other number set there
are rules of operation.
The sum and difference of complex numbers is defined by adding or subtracting
their real components ie:
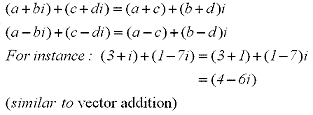
The communitive and distributive properties hold for the product of complex numbers ie:
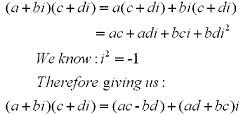
When dividing two complex numbers you are basically rationalizing the denominator
of a rational expression. If we have a complex number defined as
z =a+bi then the conjuate would be 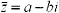 .
See the following example: .
See the following example:
Example:
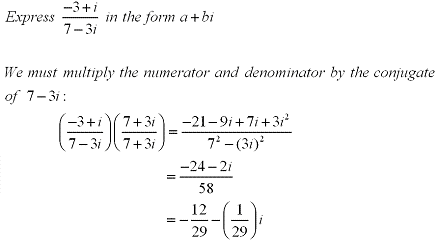
Conjugates
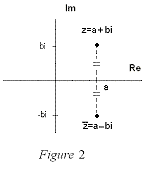
The geometric inperpretation of a complex conjugate is the reflection along the real axis.
This can be seen in the figure below where z = a+bi is a complex number.
Listed below are also several properties of conjugates.
Properties:
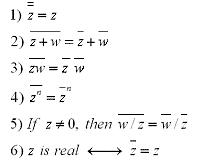
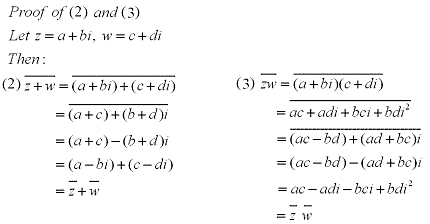
Absolue Value/Modulus
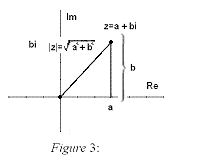
The distance from the origin to any complex number is the absolute value or modulus.
Looking at the figure below we can see that Pythagoras' Theorem gives us a formula to
calculate the absolute value of a complex number z = a+bi
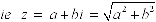
And from this we get:
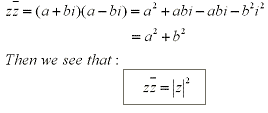
This explains why rationalizing the denominator using conjugates works in general for
complex quotients.
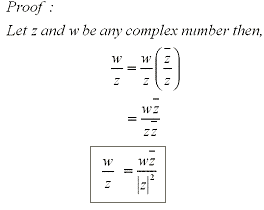
There are also some properties of absolute values dealing with complex numbers.
These are:
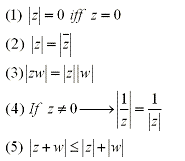
Polar Form
Along with being able to be represented as a point (a,b) on a graph, a complex number
z = a+bi can also be represented in polar form as written below:
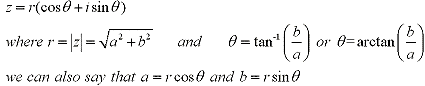
Note: The Arg(z) is the angle 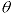 , and that this angle is only unique between
, and that this angle is only unique between 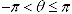 which
is called the primary angle. Adding which
is called the primary angle. Adding 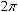
Example:
Using the principle argument, write the following complex number in its polar coordinates.
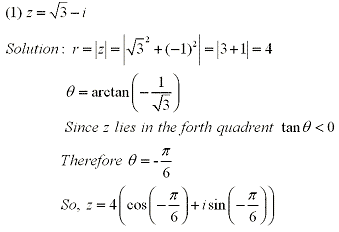
Multiplication and division can be given geometric interpretations and new insight when looking at polar forms:
Let 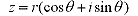 and and 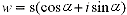 be complex numbers. be complex numbers.
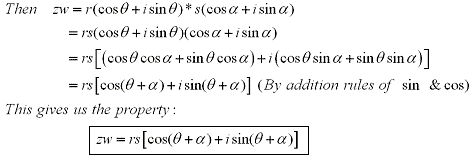
We can see from this that in order to multiply two complex numbers we must multiply the length
or absolute values together and add the arguments.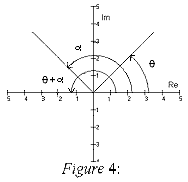
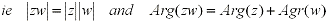
In the case of division, it is similarly shown that:
by using the subtration rule of sine and cosine, as apose to multipling the lengths we divide
and as apose to adding the arguments, we subtract.
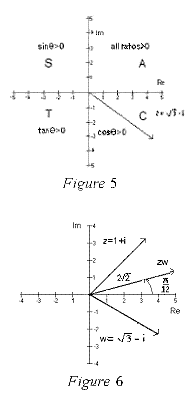
Example:
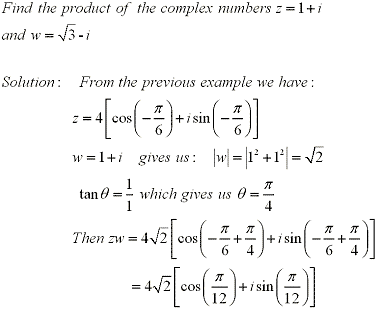
DeMoivre's Theorem
DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's
polar form.
Looking at 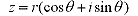 from the eariler formula we can find (z)(z) easily: from the eariler formula we can find (z)(z) easily:
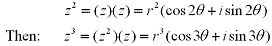
Which brings us to DeMoivre's Theorem:
If 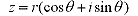 and n are positive integers then and n are positive integers then 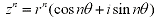
Basically, in order to find the nth power of a complex number we take the nth power
of the absolute value or length and multiply the argument by n.
Example:
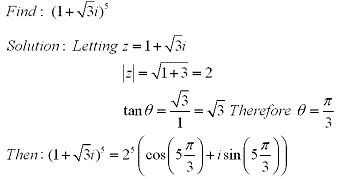
Working backwards we can also use DeMoivre's Theorem to find the nth root. Let
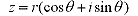 and n be a positive integer.Then z has n distinct nth roots given by: and n be a positive integer.Then z has n distinct nth roots given by:
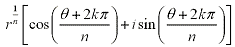
where k = 0, 1, 2, ... , n-1
To show this we let 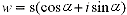 and and 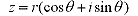 where where 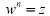 . .
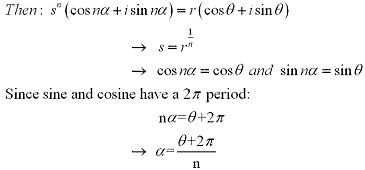
Example:
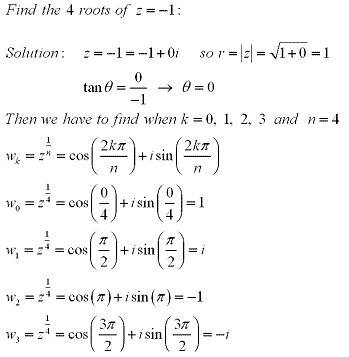
Euler's Fomula
From Calculus, we know the functions ex, sin x and cos x have power series expansions
or Taylor series.
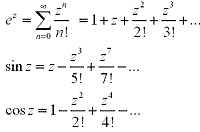
When looking at complex numbers it is interesting to see that the power series for
ez allows z to be complex and
obeys the usual rules for exponents. In particular it holds true that:
ez1+z2 =
ez1z2
letting z = iy where i is imaginary and y is a real number
From the fact that:
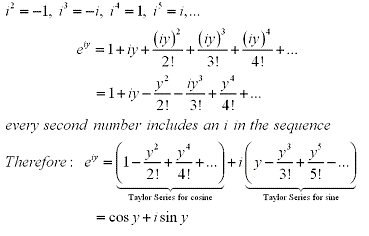
This gives us the result of Euler's Formula
eiy = cos y + isin y
Then we can also define z as: 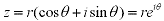
Example:
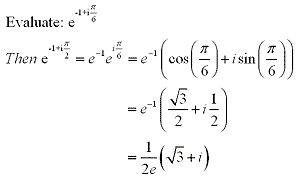
It is also important to mention that if 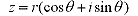 and and 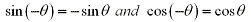
From tringonometry we can then say:
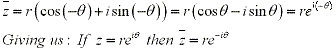
NOTE: This website has
been designed for and tested for functionality on Internet Explorer
6.0, Netscape Navigator 7.2, Netscape Browser 8.0,
and
Mozilla Firefox 1.0. Other browsers may not display information
correctly, although future versions of the abovementioned browsers
should function properly.
|

